Answer:
The function is increasing in the interval (-5,∞)
Explanation:
we have
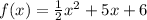
This is a vertical parabola open upward
The vertex represent a minimum
The vertex is the point (-5,-6.5)
The domain is all real numbers
The range is the interval [-6.5,∞)
so
At the left of the x-coordinate of the vertex the function is decreasing and at the right of the x-coordinate of the vertex the function is increasing
therefore
The function is increasing in the interval (-5,∞) and the function is decreasing in the interval (-∞,-5)