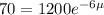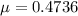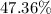Question

An insect population dies of exponentially and is governed by the equation p′=−µp, where µ is the mortality rate. If 1200 insects hatch, and only 70 remain after 6 days, what is the mortality rate?.

Answer 1

`47.36\%`

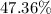
Explanation:

The equation that governs how the insect population dies is

`p' = - \mu p`

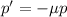
We need to solve this differential equation for p.

We separate variables to get:

`(p')/(p) = - \mu`

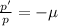
We integrate both sides to get:

`\int(p')/(p) dt = - \mu \int \: dt`

`ln( |p| ) = - \mu \: t + ln(k)`

`p = c{e}^( \ - ut)`

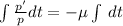
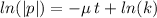
If 1200 insects hatch, and only 70 remain after 6 days,

Then we have:

`70 = 1200 {e}^( - 6 \mu)`

`(70)/(1200) = {e}^( - 6 \mu)`

`- 6 \mu = ln( (7)/(120) )`

`\mu = (ln( (7)/(120) ) )/( - 6)`

`\mu = 0.4736`

`47.36\%`