Complete Question:
The rectangle below has an area of x^2-6x-7 square meters and a width of x-7 meters. What expression represents the length of the rectangle?
Answer:
The expression represents the length of the rectangle is (x + 1) meter
Solution:
Given that,

TO FIND: LENGTH = ?
We know that,
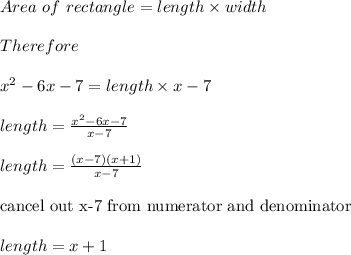
Thus expression represents the length of the rectangle is (x + 1) meter