Question

A bottler of drinking water fills plastic bottles with a mean volume of 1,000 milliliters (mL) and standard deviation The fill volumes are normally distributed. What proportion of bottles have volumes greater than

Answer 1

To find the proportion of bottles with more than 994 mL, calculate the z-score and use a z-table. Approximately 93.32% of bottles are filled with more than 994 mL.

Step-by-step explanation:

To determine the proportion of bottles with volumes greater than 994 mL, we need to use the properties of the standard normal distribution. The mean volume of a bottle is given as 1000 mL with a standard deviation of 4 mL. We first calculate the z-score for 994 mL, which is the number of standard deviations 994 mL is from the mean.

Z = (X - μ) / σ = (994 mL - 1000 mL) / 4 mL = -1.5

Using a z-table or standard normal distribution calculator, we can find the proportion of the area to the right of z = -1.5, which represents the proportion of bottles filled with more than 994 mL. The area to the right of z = -1.5 is approximately 0.9332. Therefore, about 93.32% of the bottles are expected to have volumes greater than 994 mL.

Answer 2

84.13% of bottles will have volume greater than 994 mL

Step-by-step explanation:

Mean volume = u = 1000

Standard deviation =
`\sigma` = 6

We need to find the proportion of bottles with volume greater than 994. So our test value is 994. i.e.

x = 994

Since the data is normally distributed we will use the concept of z-score to find the required proportion. First we convert 994 to its equivalent z-score, then using the z-table we will find the corresponding value of proportion. The formula to calculate the z score is:

`z=(x-u)/(\sigma)`

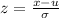
Substituting the values, we get:

`z=(994-1000)/(6)=-1`

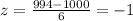
This means 994 is equivalent to a z score of -1. Now we will find the proportion of z values which are greater than -1 from the z table.

i.e. P(z > -1)

From the z-table this value comes out to be:

P(z >- 1) = 1 - P(z < -1) = 1 - 0.1587 = 0.8413

Since, 994 is equivalent to a z score of -1, we can write that proportion of values which will be greater than 994 would be:

P( X > 994 ) = P( z > -1 ) = 0.8413 = 84.13%