Answer:
7. μ=204.9 and σ=5.4968
8. μ=75.9 and σ=0.7136
9. p=0.9452
Explanation:
7. - Given that the population mean =204.9 and the standard deviation is 81.90 and the sample size n=222.
-The sample mean,
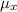 is calculated as:
is calculated as:
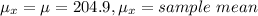
-The standard deviation,
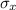 is calculated as:
is calculated as:
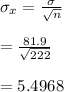
8. For a random variable X.
-Given a X's population mean is 75.9, standard deviation is 9.6 and a sample size of 181
-#The sample mean,
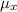 is calculated as:
is calculated as:
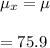
#The sample standard deviation is calculated as follows:
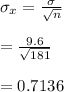
9. Given the population mean, μ=135.7 and σ=88 and n=59
#We calculate the sample mean;
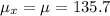
#Sample standard deviation:
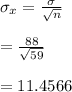
#The sample size, n=59 is at least 30, so we apply Central Limit Theorem:
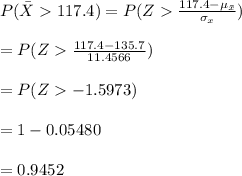
Hence, the probability of a random sample's mean being greater than 117.4 is 0.9452