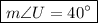Answer:
In this context:
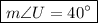
Step-by-step explanation:
Hello! Remember you have to write complete questions in order to get good and exact answers. Here you haven't provided any diagram, so I'll assume ΔSTU and ΔDEF are similar. Two triangles are similar if and only if their corresponding angles are congruent and their corresponding sides are in proportion.
So:
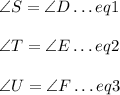
We also know:
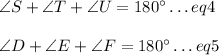
Suppose we know:
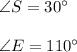
Then, by eq2:
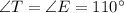
By substituting ∠S and ∠T into eq4:
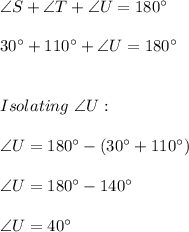
Finally: