Question

Prove: If a point on a circle is equidistant from two radii, then the radius from the point bisects the angle formed by the two given radii.

Answer 1

see the explanation

Explanation:

see the attached figure to better understand the problem

we have that

OA+OB=radii of circle O

Point P is equidistant from radii OA and OB ----> given problem

so

PA=PB

OP is a common side

Triangle OAP is congruent to Triangle OBP by SSS Postulate Theorem

Remember that

If two triangles are congruent, then its corresponding sides and its corresponding angles are congruent

That means

`m\angle POA=m\angle POB`

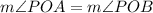
therefore

The radius from the point (PO) bisects the angle formed by the two given radii (angle ∠AOB)