Question

n a study of the accuracy of fast food​ drive-through orders, Restaurant A had 314 accurate orders and 61 that were not accurate. a. Construct a 90​% confidence interval estimate of the percentage of orders that are not accurate. b. Compare the results from part​ (a) to this 90​% confidence interval for the percentage of orders that are not accurate at Restaurant​ B: 0.147less thanpless than0.206. What do you​ conclude?

Answer 1

a. 0.1576<p<0.2310

b. The two restaurants likely have similar order rates which are inaccurate.

Explanation:

a. We first calculate the proportion,
`\hat p`:

`\hat p=(61)/(314)\\\\=0.1943`

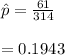
-We use the z-value alongside the proportion to calculate the margin of error:

`MOE=z\sqrt{(\hat p(1-\hat p))/(n)}\\\\=1.645* \sqrt{(0.1943(1-0.1943))/(314)}\\\\=0.0367`

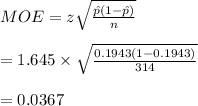
The confidence interval at 90% is then calculated as:

`CI=\hat p\pm MOE\\\\=0.1943\pm 0.0367\\\\=[0.1576,0.2310]`

Hence, the confidence interval at 90% is [0.1576,0.2310]

b. From a above, the calculated confidence interval is 0.1576<p<0.2310

-We compare the calculated CI to the stated CI of 0.147<p<0.206

-The two confidence intervals overlap each other and have the same value for 0.1576<p<0.206

-Hence, we conclude that the two restaurants likely have similar order rates which are inaccurate.