Answer:
The speed of the box at the top of the hill will be 5.693m/s.
Step-by-step explanation:
The kinetic energy of the box at the bottom of the hill is
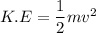
putting in
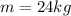 and
and
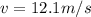 we get
we get
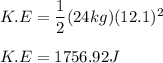
Now, the potential energy this box gains as it rises
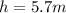 up the hill is
up the hill is

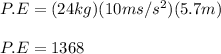
Therefore, the energy left
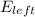 in the box at the top if the hill will be
in the box at the top if the hill will be
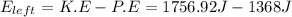

This left-over energy must appear as the kinetic energy of the box at the top of the hill (where else could it go? ); therefore,
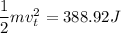
putting in numbers and solving for
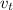 we get:
we get:
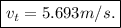
Thus, the speed of the box at the top of the hill is 5.693m/s.