Given:
It is given that LON is a straight line. The measure of ∠LOM = (4x + 30)° and the measure of ∠MON = (8x + 90)°
We need to determine the value of m∠MON
Value of x:
Since, LON is a straight line and the angles LOM and MON are linear pairs of angles.
Since, linear pair of angles add up to 180°
Thus, we have;

Substituting the values, we get;
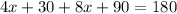
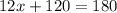
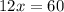

Thus, the value of x is 5.
Value of m∠MON:
The measure of ∠MON can be determined by substituting x = 5 in the expression (8x + 90)°, we have;

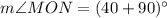

Thus, the measure of ∠MON is 130°