Answer:
It takes approximately 0.009 seconds for the capacitor to discharge to half its original charge.
Step-by-step explanation:
Recall that the capacitor discharges with an exponential decay associated with the time constant for the circuit (
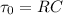 ) which in our case is;
) which in our case is;
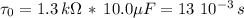 (13 milliseconds)
(13 milliseconds)
Recall as well the expression for the charge in the capacitor (from it initial value
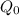 , as it discharges via a resistor R:
, as it discharges via a resistor R:
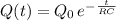
So knowing that the capacitor started with a charge of 30
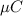 and reduced after a time "t" to 30
and reduced after a time "t" to 30
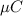 , and knowing from our first formula what the RC of the circuit is, we can solve for the time elapsed using the charge as function of time equation shown above:
, and knowing from our first formula what the RC of the circuit is, we can solve for the time elapsed using the charge as function of time equation shown above:
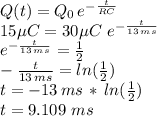
In seconds this is approximately 0.009 seconds