Question

An exam consists of 4 true/false questions and 6 multiple-choice questions with a, b, c, d, and e as

options. How many different ways could the exam be completed if someone randomly answered the
questions?

Answer 1

Explanation:

To answer this problem, you break the answer into two parts, one part for the true/false section and another part for the multiple-choice section.

True/False

There are 2 ways to answer each of the 4 true/false questions, T or F.

The number of ways to answer the trur/false section is
`2*2*2*2=2^4=16`.

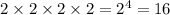Multiple-Choice

There are 5 ways to answer each question so the number of ways to answer this section is

`5*5*5*5*5=5^6=15625`

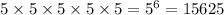
You can answer the T/F section in 16 ways and the M/C section in 15625 ways, so the entire exam can be answered in

`16*15625=250000` ways!

It's mind-boggling that only 1 of those ways gets a score of 100%!