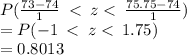Question

Suppose a simple random sample of size nequals36 is obtained from a population with mu equals 74 and sigma equals 6. ​(a) Describe the sampling distribution of x overbar. ​(b) What is Upper P (x overbar greater than 75.9 )​? ​(c) What is Upper P (x overbar less than or equals 71.95 )​? ​(d) What is Upper P (73 less than x overbar less than 75.75 )​?

Answer 1

Part a)

The simple random sample of size n=36 is obtained from a population with

`\mu = 74`

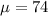
and

`\sigma = 6`

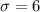
The sampling distribution of the sample means has a mean that is equal to mean of the population the sample has been drawn from.

Therefore the sampling distribution has a mean of

`\mu = 74`

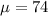
The standard error of the means becomes the standard deviation of the sampling distribution.

`\sigma_ { \bar X } = ( \sigma)/( √(n) ) \\ \sigma_ { \bar X } = ( 6)/( √(36) ) = 1`

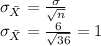
Part b) We want to find

`P(\bar X \:>\:75.9)`

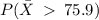
We need to convert to z-score.

`P(\bar X \:>\:75.9) = P(z \:>\: (75.9 - 74)/(1) ) \\ = P(z \:>\: (75.9 - 74)/(1) ) \\ = P(z \:>\: 1.9) \\ = 0.0287`

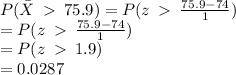
Part c)

We want to find

`P(\bar X \: < \:71.95)`

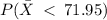
We convert to z-score and use the normal distribution table to find the corresponding area.

`P(\bar X \: < \:71.95) = P(z \: < \: (71.9 5- 74)/(1) ) \\ = P(z \: < \: (71.9 5- 74)/(1) ) \\ = P(z \: < \: - 2.05) \\ = 0.0202`

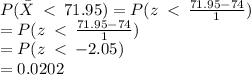
Part d)

We want to find :

`P(73\:<\bar X <\: 75.75)`

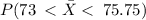
We convert to z-scores and again use the standard normal distribution table.

`P( (73 - 74)/(1) \:< \: z <\: (75.75 - 74)/(1) ) \\ = P( - 1\:< \: z <\: 1.75 ) \\ = 0.8013`