Question

PLZ HELP ME
I appreciate any help, especially if you can show me how you got the answer

Answer 1

Some calculus, a little better than the usual slopes and distances.

L'Hopital applies because the numerator is sin 0 = 0 and the denominator is ln(2 e^0 - 1) = ln 1 = 0 so we have 0/0, case number one for L'Hopital.

`(d\ \sin t)/(dt) = \cos t`

`(d\ \ln(2e^t -1 ))/(dt) = (1)/(2e^t - 1) \cdot 2e^t= (2e^t)/(2e^2 - 1)`

`\displaystyle \lim_(t \to 0) (\sin t)/(\ln(2e^t -1)) =\lim_(t \to 0) (\cos t )/( 2e^t/ (2e^t - 1) ) =\lim_(t \to 0) ( (2e^t - 1) \cos t )/( 2e^t)`

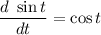
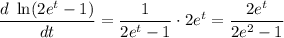
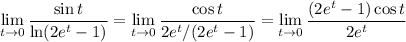
Evaluating the latter form at t=0 we get

`\displaystyle \lim_(t \to 0) (\sin t)/(\ln(2e^t -1)) = ((2e^0 -1) \cos 0)/(2e^0) = (1)/(2)`

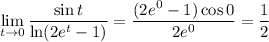
Answer: C 1/2