Question

Which dimensions can create only one unique triangle?

three angles measuring 25 degrees, 65 degrees, and 90 degrees
three angles measuring 50 degrees, 50 degrees, and 50 degrees
three sides measuring 5 in., 12 in., and 14 in.
three sides measuring 4 ft, 8 ft, and 14 ft

Answer 1

Three sides measuring 5 in., 12 in., and 14 in.

Step-by-step explanation:

First of all, you need to know some facts about every triangle:

FIRST FACT:

If two sides of a triangle are
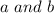`a \ and \ b`, then the third side must be less than
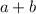`a+b`. Why? because if its length is exactly
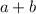`a+b`, then you can't build up a triangle, but you'll have a line segment. In other words:

`a<b+c \\ \\ b<a+c \\ \\ c<a+b`

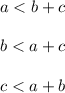
SECOND FACT:

The internal angles of any triangle add up to 180°. So if ∠A, ∠B and ∠C are the internal angles of a triangle, then:

`\angle A +\angle B+ \angle C=180^(\circ)`

__________________________

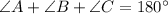
So let's analyze each case:

Case 1. Three angles measuring 25 degrees, 65 degrees, and 90 degrees :

`\angle A=25^(\circ) \\ \\ \angle B=65^(\circ) \\ \\ \angle C=90^(\circ) \\ \\ \\ \angle A +\angle B+ \angle C=25^(\circ)+65^(\circ)+90^(\circ)=185^(\circ) \\eq 180^(\circ)`

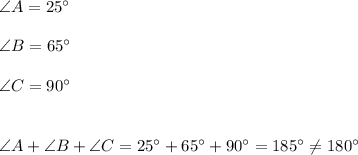
The sum is greater than 180 degrees, so these angles can't form a triangle

Case 2. Three angles measuring 50 degrees, 50 degrees, and 50 degrees

`\angle A=50^(\circ) \\ \\ \angle B=50^(\circ) \\ \\ \angle C=50^(\circ) \\ \\ \\ \angle A +\angle B+ \angle C=50^(\circ)+50^(\circ)+50^(\circ)=150^(\circ) \\eq 180^(\circ)`

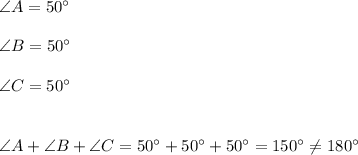
The sum is less than 180 degrees, so these angles can't form a triangle

Case 3. Three sides measuring 5 in., 12 in., and 14 in.

`a=5 \\ \\ b=12 \\ \\ c=14 \\ \\ \\ 5<12+14\rightarrow 5<26 \\ \\ 12<5+14 \rightarrow 12<19 \\ \\ 14<5+12 \rightarrow 14<17`

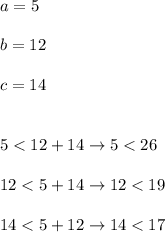
The inequalities are true, so these sides form a triangle.

Case 4: Three sides measuring 4 ft, 8 ft, and 14 ft

`a=4 \\ \\ b=8 \\ \\ c=14 \\ \\ \\ 4<8+14\rightarrow 4<22 \\ \\ 8<4+14 \rightarrow 8<18 \\ \\ 14<4+8 \rightarrow 14<12 \ NOT \ TRUE!`

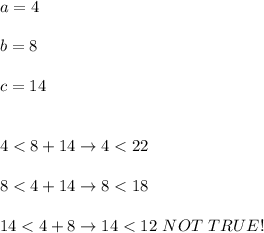
Since the third inequality is not true, then we can't form a triangle with these sides.