Answer:
EX=-$1
Explanation:
Expected Value of Probability Distribution
Assume a discrete probability distribution is

For

The expected value is

We have two possible outcomes from our random experience: The sum of the die is 7 or different from 7. If it sums 7, the player wins $9, otherwise, they lose $3. Thus
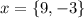
We must find the probability of having a 7. Each dice can be a 1, 2, 3 ,4 , 5, or 6. The combinations to sum 7 are 1+6, 2+5, 3+4, 4+4, 5+2, and 6+1. That is 6 possibilities out of 36 in total. The probability of having a 7 is
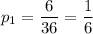
The probability of not getting 7 is the negation of the previous event
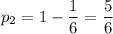
The probability set is:
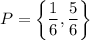
The expected value is:
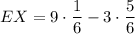

Therefore, the player can expect to lose $1