Question

In your homework, you were introduced to a game, called Under-or-Over-Seven. It has many rules. Here is the particular rule that we are going to use for this question: a pair of fair dice is rolled once, and the resulting sum determines whether the player wins or loses his/her bet; the player wins $9 if the result of the roll is exactly equal to 7 and loses $3 otherwise. Compute the expected value of this game (i.e., the expected gain or loss).

Answer 1

EX=-$1

Explanation:

Expected Value of Probability Distribution

Assume a discrete probability distribution is

`P=\{p1,p2,p3,...pn\}`

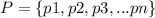
For

`X=\{x1,x2,x3,...xn\}`

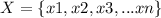
The expected value is

`EX=\sum x_i.p_i`

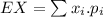
We have two possible outcomes from our random experience: The sum of the die is 7 or different from 7. If it sums 7, the player wins $9, otherwise, they lose $3. Thus

`x=\{9,-3\}`

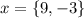
We must find the probability of having a 7. Each dice can be a 1, 2, 3 ,4 , 5, or 6. The combinations to sum 7 are 1+6, 2+5, 3+4, 4+4, 5+2, and 6+1. That is 6 possibilities out of 36 in total. The probability of having a 7 is

`\displaystyle p_1=(6)/(36)=(1)/(6)`

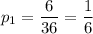
The probability of not getting 7 is the negation of the previous event

`\displaystyle p_2=1-(1)/(6)=(5)/(6)`

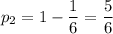
The probability set is:

`\displaystyle P=\left\{(1)/(6),(5)/(6)\right\}`

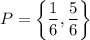
The expected value is:

`\displaystyle EX=9\cdot (1)/(6)-3\cdot (5)/(6)`

`\displaystyle EX=(3)/(2)-(5)/(2)=-1`

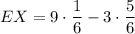
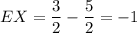
Therefore, the player can expect to lose $1