Question

You measure 50 textbooks' weights, and find they have a mean weight of 52 ounces. Assume the population standard deviation is 14.6 ounces. Based on this, construct a 90% confidence interval for the true population mean textbook weight.

Answer 1

The 90% confidence interval = 48.603 < μ < 55.397

Step-by-step explanation:

Given:

Mean = 52

Standard deviation = 14.6

Sample size, n = 50

Confidence Interval, c = 90%

c = 0.9

Significance level, α = 1 - c

= 1 - 0.9

= 0.1

Critical value, z(α/2) = z(0.05) = 1.645

Critical value = ± 1.645

Margin of error, E =
`z(\alpha /2) X (SD)/(√(n) )`

`=1.645 X(14.6)/(√(50) ) \\\\= 3.3965`

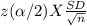
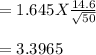
Limits of 90% confidence interval are given by:

Lower limit = μ - E

= 52 - 3.397

= 48.603

Upper limit = μ + E

= 52 + 3.397

= 55.397

Thus, 90% confidence interval = 48.603 < μ < 55.397