Question

What is the arc measure of DBC in
degrees?

Answer 1

In this context:

`\boxed{\angle DBC=x=60^(\circ)}`

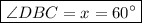
Step-by-step explanation:

Hello! Remember to write complete questions in order to get good and exact answers. Here the figure is missing so I'll assume the arc measure of DBC is given in radian and you want it in degrees. By definition, an arc's measure is the measure of its central angle being a central angle an angle between two radii in a circle. Suppose that angle measures:

`\angle DBC=(\pi)/(3)\ radian \\ \\ \\ So, \ by \ rule \ of \ three: \\\\ \\ \pi \ radian \rightarrow 180 \ degrees \\ \\ \pi/3 \ radian \rightarrow x \ degrees \\ \\ \\ x =(180\pi)/(3\pi)=60^(\circ) \\ \\ \\ Finally: \\ \\ \boxed{\angle DBC=x=60^(\circ)}`