Question

Can u show me how to simply this step by step please? This is very important. HELP!!!!!

Answer 1

Given:

`$(\left((a^(2)-b^(2))/(a b)\right))/(\left((1)/(b)-(1)/(a)\right))`

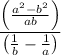
To find:

The simplified expression.

Solution:

`$(\left((a^(2)-b^(2))/(a b)\right))/(\left((1)/(b)-(1)/(a)\right))`

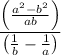
Apply the fraction rule:
`((y)/(z))/(x)=(y)/(z \cdot x)`

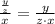
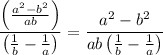`$(\left((a^(2)-b^(2))/(a b)\right))/(\left((1)/(b)-(1)/(a)\right))=(a^(2)-b^(2))/(a b\left((1)/(b)-(1)/(a)\right))` ------------ (1)

Let us simplify
`(1)/(b)-(1)/(a)`.

LCM of a and b = ab

Adjacent fraction based on the LCM

`(1)/(b)-(1)/(a)=(a)/(a b)-(b)/(a b)`

`=(a-b)/(a b)`

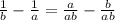
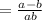
Substitute this in equation (1).

`$=(a^(2)-b^(2))/((a-b)/(a b) a b)`

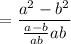
Common factor ab get canceled.

`$=(a^(2)-b^(2))/(a-b)`

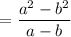
Apply the algebraic formula:
`x^(2)-y^(2)=(x+y)(x-y)`

`$=((a+b)(a-b))/(a-b)`

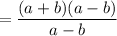
Cancel the common factor a - b, we get

`=a+b`

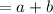
The simplified expression is a + b.