Question

Enter the slope-intercept equation of the line that has the same slope as y - 3 = (x + 3) and contains

the point (8,4). Complete the explanation of how you found the equation.
y= ;l used the general form of a line in slope-intercept form, or y=mx+
b w The
slope, m, is .Then, I substituted for x and fory into the standard form and solved
for b, which is


HELLPPP please

Answer 1

Given:

`y-3=(1)/(2)(x+3)`

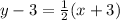
Point = (8, 4)

To find:

The slope-intercept form of the equation of the line.

Solution:

`$y-3=(1)/(2)(x+3)`

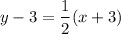
Slope of this line =
`(1)/(2)`.

Slope of the line is same as the slope of
`y-3=(1)/(2)(x+3)`.

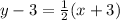Slope of the line (m) =
`(1)/(2)`

General form of line:

y = mx + b

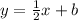`y=(1)/(2) x+b` ---------- (1)

It contains the point (8, 4). Substitute x = 8 and y = 4 in (1).

`4=(1)/(2)( 8)+b`

`4=4+b`

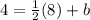
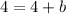
Subtract 4 from both sides, we get

b = 0

Substitute b = 0 in (1).

Equation of the line:

`y=(1)/(2) x+0`

`$y=(1)/(2) x`

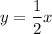
Complete the sentence:

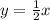`y=(1)/(2) x`; I used the general form of a line in slope-intercept form, y = mx + b. The slope, m is
`(1)/(2)`. Then I substituted 8 for x and 4 for y into the standard form and solved for b, which is 0.