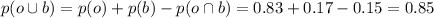Question

The manager at the local auto shop has found that the probability that a car brought into the shop requires an oil change is 0.83​, the probability that a car brought into the shop requires brake repair is 0.17​, and the probability that a car requires both an oil change and brake repair is 0.15. For a car brought into the​ shop, determine the probability that the car will require an oil change or brake repair.

Answer 1

0.85

Explanation:

Given two events A and B, the probability that either A or B occurs is given by:

`p(A\cup B) = p(A)+p(B)-p(A\cap B)`

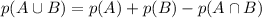
where

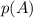`p(A)` the probability that A occurs

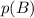`p(B)` is the probability that B occurs

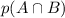`p(A\cap B)` is the probability that both A and B occur at the same time

In this problem, we know the following facts:

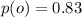`p(o) = 0.83` is the probability that the car requires an oil change

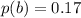`p(b)=0.17` is the probability that the car requires a brake repair

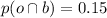`p(o\cap b) = 0.15` is the probability that the car requires both an oil change and brake repair

Therefore, the probability that either o (car requiring oil change) or b (car requiring brake repait) occur is:

`p(o\cup b)=p(o)+p(b)-p(o\cap b)=0.83+0.17-0.15 = 0.85`