Question

An object is thrown up word from the top of 160 foot building with an initial velocity of 144 ft./s. The height H of the object after T seconds is given by the quadratic equation h= -16t^2 + 144t + 160. When will the object hit the ground?

Answer 1

After 10 seconds

Explanation:

In this problem, the height of the object after t seconds is described by the function

`h(t)=-16t^2+144t+160`

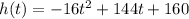
where

160 ft is the initial height of the object at t = 0

+144 ft/s is the initial velocity

`-32 ft/s^2` is the acceleration due to gravity (downward)

Here we want to find the time at which the object hits the ground, so the time t at which

`h(t)=0`

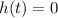
Therefore we can write

`-16t^2+144t+160 =0`

Simplifying (dividing each term by 16), we get

`-t^2+9t+10=0`

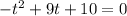
This is a second-order equation in the form

`ax^2+bx+c=0`

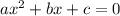
Which has solutions given by the formula

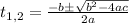`t_(1,2)=(-b\pm √(b^2-4ac))/(2a)` (2)

Here we have:

a = -1

b = 9

c = 10

Substituting into (2) we find the solutions:

`t_(1,2)=(-9\pm √(9^2-4(-1)(10)))/(2(-1))=(-9 \pm 11)/(-2)`

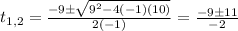
Which gives:

`t_1=10 s\\t_2 =-1 s`

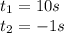
Since time cannot be negative, the only solution is

t = 10 seconds