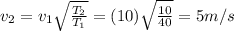Question

3. The velocity of waves on a rope under a tension of 40 N is 10 m/s. If the tension is reduced

to 10 N, what will be the new speed of the wave?
HAI

Answer 1

5 m/s

Step-by-step explanation:

The speed of a wave in a string is related to the tension in the string by the equation

`v=\sqrt{(T)/(\mu)}`

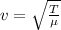
where

v is the speed of the wave

T is the tension in the string

`\mu` is the linear density of the string

We can rewrite the equation as

`(√(T))/(v)=√(\mu)`

In this problem, the tension in the string is changed; however, its linear mass density remains constant. So we can write:

`(√(T_1))/(v_1)=(√(T_2))/(v_2)`

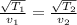
where:

T1 = 40 N is the initial tension in the string

v1 = 10 m/s is the initial speed of the wave

T2 = 10 N is the final tension in the string

Solving for v2, we find the final speed of the wave:

`v_2=v_1 \sqrt{(T_2)/(T_1)}=(10)\sqrt{(10)/(40)}=5 m/s`