Answer:
Probability that their mean weight will be between 413 grams and 464 grams is 0.8521.
Step-by-step explanation:
We are given that a particular fruit's weights are normally distributed, with a mean of 426 grams and a standard deviation of 37 grams.
Also, you pick 9 fruit at random.
Let
 = sample mean weight
= sample mean weight
The z-score probability distribution for sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean weight = 426 grams
= population mean weight = 426 grams
 = population standard deviation = 37 grams
= population standard deviation = 37 grams
n = sample of fruits = 9
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
So, probability that the mean weight of 9 fruits picked at random will be between 413 grams and 464 grams is given by = P(413 grams <
 < 464 grams) = P(
< 464 grams) = P(
 < 464 grams) - P(
< 464 grams) - P(

 413 grams)
413 grams)
P(
 < 464 grams) = P(
< 464 grams) = P(
 <
<
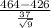 ) = P(Z < 3.08) = 0.99896
) = P(Z < 3.08) = 0.99896
P(

 413 grams) = P(
413 grams) = P(


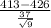 ) = P(Z
) = P(Z
 -1.05) = 1 - P(Z < 1.05)
-1.05) = 1 - P(Z < 1.05)
= 1 - 0.85314 = 0.14686
{Now, in the z table the P(Z
 x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 3.08 and x = 1.05 in the z table which has an area of 0.99896 and 0.85314 respectively.}
x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 3.08 and x = 1.05 in the z table which has an area of 0.99896 and 0.85314 respectively.}
Therefore, P(413 grams <
 < 464 grams) = 0.99896 - 0.14686 = 0.8521
< 464 grams) = 0.99896 - 0.14686 = 0.8521
Hence, the probability that their mean weight will be between 413 grams and 464 grams is 0.8521.