Question

$1500 is invested at a rate of 3% compounded monthly. Write a compound interest function to model this situation. Then find the

balance after 5 years.

Answer 1

Equation:
`F=1500(1.0025)^(12t)`

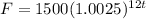
The balance after 5 years is: $1742.43

Explanation:

This is a compound growth problem . THe formula is:

`F=P(1+(r)/(n))^(nt)`

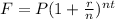
Where

F is future amount

P is present amount

r is rate of interest, annually

n is the number of compounding per year

t is the time in years

Given:

P = 1500

r = 0.03

n = 12 (compounded monthly means 12 times a year)

The compound interest formula modelled by the variables is:

`F=1500(1+(0.03)/(12))^(12t)\\F=1500(1.0025)^(12t)`

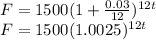
Now, we want balance after 5 years, so t = 5, substituting, we get:

`F=1500(1.0025)^(12t)\\F=1500(1.0025)^(12*5)\\F=1500(1.0025)^(60)\\F=1742.43`

The balance after 5 years is: $1742.43