Final Answer:
1) The x-intercepts of the function
 are
are
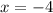 and
and
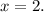
2) The y-intercept of the function
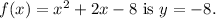
3) The equation of the axis of symmetry is
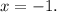
4) The vertex of the function
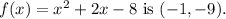
5) The graph of the function is a parabola opening upwards with the vertex at
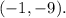
Step-by-step explanation:
1) To find the x-intercepts, set
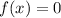 and solve for x. The quadratic equation
and solve for x. The quadratic equation
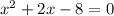 factors into
factors into
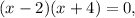 yielding x-intercepts of
yielding x-intercepts of
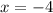 and
and
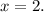
2) To find the y-intercept, set \( x = 0 \) in the function. \( f(0) = 0^2 + 2(0) - 8 = -8 \), so the y-intercept is

3) The axis of symmetry for a quadratic function in the form
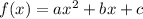 is given by
is given by
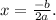 For
For
 , the axis of symmetry is
, the axis of symmetry is
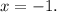
4) The vertex of a quadratic function in the form
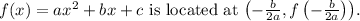 Substituting
Substituting
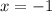 into the function, we find that the vertex is
into the function, we find that the vertex is
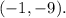
5) The graph of the function is a parabola that opens upwards, consistent with the positive coefficient of the
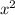 term. The vertex at (-1, -9) is the lowest point on the graph, and the parabola extends upward indefinitely from there.
term. The vertex at (-1, -9) is the lowest point on the graph, and the parabola extends upward indefinitely from there.