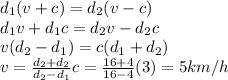Answer:
5 km/h
Explanation:
In this problem, Lashonda swam 4 km against the current. So the distance covered in this case is
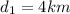
Calling
 the velocity of Lahonda without the current, and
the velocity of Lahonda without the current, and
 the velocity of the current, in this situation Lahonda's velocity is
the velocity of the current, in this situation Lahonda's velocity is

So we can write:

where
 is the time taken to cover the distance.
is the time taken to cover the distance.
When Lashonda swims with the current, her velocity is
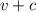
So we can write
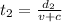
where
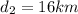 is the distance covered in this case, and
is the distance covered in this case, and
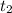 the time taken.
the time taken.
The velocity of the current is
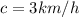
Since Lashonad takes the same time to cover the two distances,
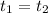
So we can write

And solving for v, we find Lashonda's velocity without the current: