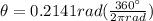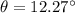Question

Monochromatic light of wavelength 491 nm illuminates two parallel narrow slits 6.93 μm apart. Calculate the angular deviation of the third-order (for m = 3) bright fringe (a) in radians and (b) in degrees.

Answer 1

To solve this problem we will apply the concepts related to the double slit experiment. Here we test a relationship between the sine of the deviation angle and the distance between slit versus wavelength and the bright fringe order. Mathematically it can be described as,

`dsin\theta = m\lambda`

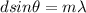
Here,

d = Distance between slits

m = Any integer which represent the order number or the number of repetition of the spectrum

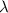`\lambda` = Wavelength

`\theta` = Angular deviation

Replacing with our values we have,

`(6.93*10^(-6)) sin\theta = (3)(491*10^(-9))`

`\theta = sin^(-1) (((3)(491*10^(-9))/(6.93*10^(-6)) ))`

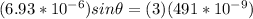
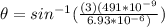
Part A)

`\theta = 0.2141rad`

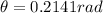
PART B)

`\theta = 0.2141rad((360\°)/(2\pi rad))`

`\theta = 12.27\°`