Question

Multiplying Polynomials and Simplifying Expressions

Answer 1

Given:

Polynomials:
`a+3 \text { and }-2 a^(2)+15 a+6 b^(2)`

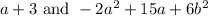
To find:

The product of the polynomials.

Solution:

`(a+3)(-2 a^(2)+15 a+6 b^(2))`

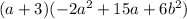
Using distributive property:
`x(y+z)=xy+xz`

`(a+3)(-2 a^(2)+15 a+6 b^(2))=a(-2 a^(2)+15 a+6 b^(2))+3(-2 a^(2)+15 a+6 b^(2))`

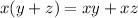
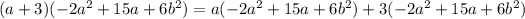
Now multiply each of the first term with each of the second term.

`=a\left(-2 a^(2)\right)+a \cdot 15 a+a \cdot 6 b^(2)+3\left(-2 a^(2)\right)+3 \cdot 15 a+3 \cdot 6 b^(2)`

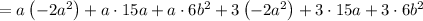
Applying plus minus rule:
`+(-x)=-x`

`=-2 a^(2) \cdot a+15 a \cdot a+6 a\cdot b^(2)-3 \cdot 2 a^(2)+3 \cdot 15 a+3 \cdot 6 b^(2)`

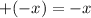
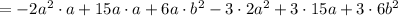
Apply the exponent rule:
`x^(n) \cdot x^(m)=x^(n+m)`

`=-2 a^(3)+15 a^2+6 a b^(2)-6 a^(2)+45 a+18 b^(2)`

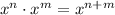
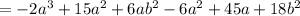
Add or subtract the like terms:

`=-2 a^(3)+15 a^2-6a^2+6 a b^(2)+45 a+18 b^(2)`

`=-2 a^(3)+9 a^(2)+6 a b^(2)+45 a+18 b^(2)`

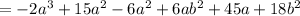
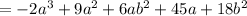
Arrange in the order.

`=-2 a^(3)+9 a^(2)+45 a+6 a b^(2)+18 b^(2)`

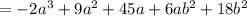
The product of
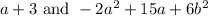
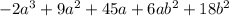`a+3 \text { and }-2 a^(2)+15 a+6 b^(2)`
`-2 a^(3)+9 a^(2)+45 a+6 a b^(2)+18 b^(2)`.