I suppose you're supposed to prove that set intersection is distributive across a union,
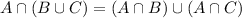
Two sets are equal if they are subsets of one another. To prove a set
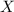 is a subset of another set
is a subset of another set
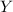 , you have to show that any element
, you have to show that any element
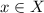 also belongs to
also belongs to
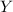 .
.
Let
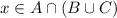 . By definition of intersection, both
. By definition of intersection, both
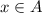 and
and
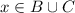 . By definition of union, either
. By definition of union, either
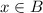 or
or
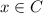 . If
. If
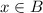 , then clearly
, then clearly
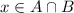 ; if
; if
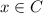 , then
, then
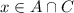 . Either way,
. Either way,
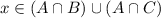 . Hence
. Hence
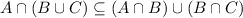 .
.
The proof in the other direction uses the same sort of reasoning. Let
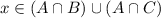 . Then either
. Then either
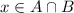 or
or
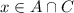 . If
. If
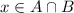 , then both
, then both
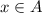 and
and
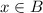 ; if
; if
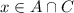 , then both
, then both
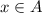 and
and
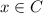 . So certainly
. So certainly
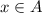 , and either
, and either
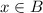 or
or
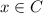 so that
so that
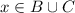 . Hence
. Hence
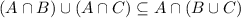 .
.
Both sets are subsets of one another, so they are equal.