Answer:
The exponential form is 49 to the power of one-half equals 7 ⇒ 4th answer
Step-by-step explanation:
The exponential equation of
 is
is
 , where b is the base, n is the exponent of b and m is the value of
, where b is the base, n is the exponent of b and m is the value of
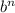
Ex: If
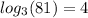 , that means b = 3 , n = 4 and m = 81, then its exponential form is
, that means b = 3 , n = 4 and m = 81, then its exponential form is
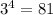
Now let us solve the question
∵ The equation is
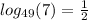
∴ The base is 49
∴ The exponent is

∴ The answer is 7
- Substitute them in the form of the exponential form
∴ The exponential form is
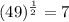
The exponential form is 49 to the power of one-half equals 7