Question

A 60kg bicyclist (including the bicycle) is pedaling to the

right, causing her speed to increase at a rate of 3.1 m/s2,
despite experiencing a 60N drag. Neglect any friction
impeding her motion.

How many forces are acting on the bicyclist?

What is the magnitude of the net force on the bicyclist?

How much force is the bicyclist generating through her
pedaling?

Answer 1

Two forces are acting on the bicyclist: the 60 N drag force and the pedaling force. The magnitude of the net force is 186 N calculated using Newton's second law. The force generated by the bicyclist through pedaling is 246 N.

Step-by-step explanation:

To determine the number of forces acting on the bicyclist, we must consider both the drag force and the force generated by the cyclist's pedaling. Two forces are acting on the bicyclist: the pedaling force she generates and the 60N drag force opposing her motion.

To find the magnitude of the net force, we use Newton's second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma). We know the mass (m) is 60 kg and the acceleration (a) is 3.1 m/s2, so the net force (Fnet) can be calculated as:

Fnet = m × a
Fnet = 60 kg × 3.1 m/s2
Fnet = 186 N

The pedaling force the bicyclist is generating can be found by adding the drag force to the net force since they are in opposite directions:

Fpedaling = Fnet + Fdrag
Fpedaling = 186 N + 60 N
Fpedaling = 246 N

Thus, the bicyclist generates a pedaling force of 246 Newtons.

Answer 2

a) 4 forces

b) 186 N

c) 246 N

Step-by-step explanation:

a)

Let's count the forces acting on the bicylist:

1) Weight (
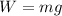`W=mg`): this is the gravitational force exerted on the bicyclist by the Earth, which pulls the bicyclist towards the Earth's centre; so, this force acts downward (m = mass of the bicyclist, g = acceleration due to gravity)

2) Normal reaction (N): this is the reaction force exerted by the road on the bicyclist. This force acts vertically upward, and it balances the weight, so its magnitude is equal to the weight of the bicyclist, and its direction is opposite

3) Applied force (
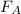`F_A`): this is the force exerted by the bicylicist to push the bike forward. Its direction is forward

4) Air drag (
`R`): this is the force exerted by the air on the bicyclist and resisting the motion of the bike; its direction is opposite to the motion of the bike, so it is in the backward direction

So, we have 4 forces in total.

b)

Here we can find the net force on the bicyclist by using Newton's second law of motion, which states that the net force acting on a body is equal to the product between the mass of the body and its acceleration:

`F_(net)=ma`

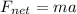
where

`F_(net)` is the net force

m is the mass of the body

a is its acceleration

In this problem we have:

m = 60 kg is the mass of the bicyclist

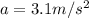`a=3.1 m/s^2` is its acceleration

Substituting, we find the net force on the bicyclist:

`F_(net)=(60)(3.1)=186 N`

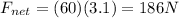
c)

We can write the net force acting on the bicyclist in the horizontal direction as the resultant of the two forces acting along this direction, so:

`F_(net)=F_a-R`

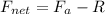
where:

`F_(net)` is the net force

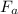`F_a` is the applied force (forward)

`R` is the air drag (backward)

In this problem we have:

`F_(net)=186 N` is the net force (found in part b)

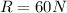`R=60 N` is the magnitude of the air drag

Solving for
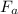`F_a`, we find the force produced by the bicyclist while pedaling:

`F_a=F_(net)+R=186+60=246 N`