Given:
Sphere and cylinder have same radius and height.
Volume of the cylinder = 48 cm³
To find:
The volume of the sphere.
Solution:
Radius and height of cylinder are equal.
⇒ r = h
Volume of cylinder:
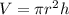
Substitute the given values.
 (since r = h)
(since r = h)
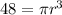
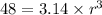
Divide by 3.14 on both sides.

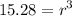
Taking cube root on both sides, we get
2.48 = r
The radius of the cylinder is 2.48 cm.
Sphere and cylinder have same radius and height.
Volume of sphere:

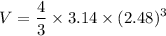
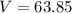
The volume of the sphere is 63.85 cm³.