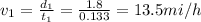Question

The average speed of a car decreased by 3 miles per hour every successive 8-minute interval. If the car traveled 4.8 miles in the sixth 8-minute interval, what was the average speed of the car, in miles per hour, in the first 8-minute interval?

Answer 1

13.5 mi/h

Explanation:

The average speed of the car can be written as

`v=(d)/(t)`

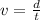
where

d = 4.8 miles is the total distance covered

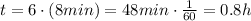`t=6\cdot (8 min) = 48 min \cdot (1)/(60)=0.8 h` is the time elapsed

So the average speed is

`d=(4.8)/(0.8)=6 mi/h`

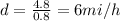
We also know that the total time consists of 6 8-minutes interval, and the speed of the car decreased by 3 mi/h each interval.

Calling
`v_1` the average speed in the 1st interval, we have:

`v_2=v_1-3\\v_3=v_1-6\\v_4=v_1-9\\v_5=v_1-12\\v_6=v_1-15`

The average speed in each interval can be written as
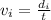`v_i=(d_i)/(t)`, where
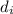`d_i` is the distance covered in each interval and
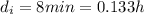`d_i = 8 min =0.133 h` is the duration of each interval, so we can write

`(d_2)/(t)=(d_1)/(t) -3 \rightarrow d_2 = d_1 -3t`

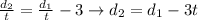
And similarly,

`d_3=d_1-6t\\d_4=d_1-9t\\d_5=d_1-12t\\d_6=d_1-15t`

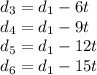
Since the total distance is
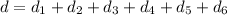`d=d_1+d_2+d_3+d_4+d_5+d_6`, we have:

`d=6d_1 - 3t-6t-9t-12t-15t=6d_1-45t`

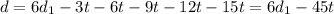
And since we know that

d = 4.8 miles

and t = 0.133h, we can find d1:

`d_1=(d+45t)/(6)=(4.8+(45)(0.133))/(6)=1.8 mi`

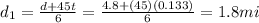
So the average speed in the first 8-minute interval is:

`v_1=(d_1)/(t_1)=(1.8)/(0.133)=13.5 mi/h`