Answer:
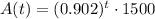
![[km^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/3p9jb2ocat0p09qe6qtlvntetag6ggczqt.png)
Explanation:
In this problem, the initial area of the forest at time t = 0 is
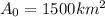
After every year, the area of the forest decreases by 9.8%: this means that the area of the forest every year is (100%-9.8%=90.2%) of the area of the previous year.
So for instance, after 1 year, the area is
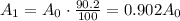
After 2 years,

And so on. So, after t years, the area of the forest will be

And by substituting the value of A0, we can find an explicit expression:
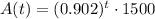
![[km^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/3p9jb2ocat0p09qe6qtlvntetag6ggczqt.png)