Given:
Deposit (P) = £2000
Rate of interest (r) = 3%
Time (t)= 2 years
Number of time interest calculated per year (n) = 1
To find:
Amount in the account after 2 years
Solution:
Compound interest formula:
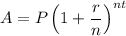
Substitute the given values.
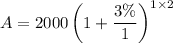
To convert percentage into fraction divide by 100.
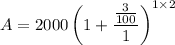
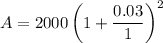
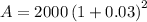
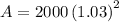
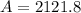
Therefore, £2121.8 will be in the account after 2 years.