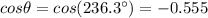Question

What is the value of cosθ given that (−2, −3) is a point on the terminal side of θ ?

Answer 1

-0.555

Explanation:

The terminal point of the vector in this problem is

(-2,-3)

So, it is in the 3rd quadrant.

We want to find the angle
`\theta` that gives the direction of this vector.

We can write the components of the vector along the x- and y- direction as:

`v_x = -2\\v_y = -3`

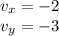
The tangent of the angle will be equal to the ratio between the y-component and the x-component, so:

`tan \theta = (v_y)/(v_x)=(-3)/(-2)=1.5\\\theta=tan^(-1)(1.5)=56.3^(\circ)`

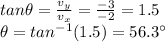
However, since we are in the 3rd quadrant, the actual angle is:

`\theta=180^(\circ) + 56.3^(\circ) = 236.3^(\circ)`

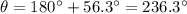
So now we can find the cosine of the angle, which will be negative:

`cos \theta = cos(236.3^(\circ))=-0.555`