a) Increase
b) Unchanged
c) Increase
Step-by-step explanation:
a)
The charge on a capacitor charging in a RC circuit connected to a battery follows the exponential equation:
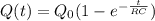
where
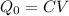 is the final charge stored in the capacitor, where C is the capacitance and V is the voltage of the battery
is the final charge stored in the capacitor, where C is the capacitance and V is the voltage of the battery
t is the time
R is the resistance of the circuit
The capacitor reaches 90% of its final charge when
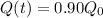
Substituting and re-arranging the equation, we find:
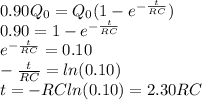
We see that if we double the RC constant, then
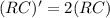
So the time taken will double as well:
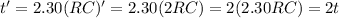
So, the answer is "increase"
b)
In this second part, the battery voltage is doubled.
According to the equation written in part a),
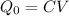
this means also that the final charge stored on the capacitor will also double.
However, the equation that gives us the time needed for the capacitor to reach 90% of its full charge is
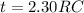
We see that this equation does not depend at all on the voltage of the battery.
Therefore, if the battery voltage is doubled, the final charge on the capacitor will double as well, but the time needed for the capacitor to reach 90% of its charge will not change.
So the correct answer is
"unchanged"
c)
In this case, a second resistor is added in series with the original resistor of the circuit.
We know that for two resistors in series, the total resistance of the circuit is given by the sum of the individual resistances:
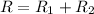
Since each resistance is a positive value, this means that as we add new resistors, the total resistance of the circuit increases.
Therefore in this problem, if we add a resistor in series to the original circuit, this means that the total resistance of the circuit will increase.
The time taken for the capacitor to reach 90% of its final charge is still
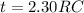
As we can see, this time is directly proportional to the resistance of the circuit, R: therefore, if we add a resistor in series, the resistance of the circuit will increase, and therefore this time will increase as well.
So the correct answer is
"increase"