Question

The labor force participation rate is the number of people in the labor force divided by the number of people in the country who are of working age and not institutionalized. The BLS reported in February 2012 that the labor force participation rate in the United States was 63.7% (Calculatedrisk). A marketing company asks 120 working-age people if they either have a job or are looking for a job, or, in other words, whether they are in the labor force. What are the expected value and the standard error for a labor participation rate in the company's sample?

Answer 1

Expected value=77 people

Standard error=0.0040

Explanation:

-Given the proportion is, p=0.67

-The expected value can be calculated as:

`Expected \ Value=np\\\\=120* 0.637\\\\=76.44\approx 77`

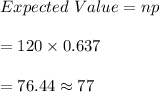
#The standard deviation is calculated as:

`\sigma_p=\sqrt{(p(1-p))/(n)}\\\\=\sqrt{(0.637(1-0.637))/(120)}\\\\=0.0439`

#We use this calculated standard deviation to calculate the standard error:

`SE=(\sigma_p)/(√(n))\\\\=(0.0439)/(√(120))\\\\=0.0040`

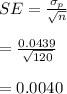
Hence, the sample has an expected value of approximately 77 people and a standard error of 0.0040