Answer:
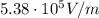
Step-by-step explanation:
At first, the 6Li ions are accelerated by the potential difference, so their gain in kinetic energy is equal to the change in electric potential energy; so we can write:

where
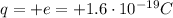 is the charge of one 6Li ion
is the charge of one 6Li ion
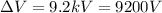 is the potential difference through which they are accelerated
is the potential difference through which they are accelerated
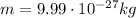 is the mass of each ion
is the mass of each ion
v is the final speed reached by the ions
Solving for v, we find:
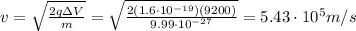
After that, the ions pass into a region with a uniform magnetic field of strength
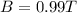
The magnetic field exerts a force perpendicular to the direction of motion of the ions, and this force is given by
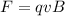
In order to make the ions passing through undeflected, there should be an electric force balancing this magnetic force. The electric force is given by
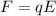
where E is the strength of the electric field.
Since the two forces must be balanced,
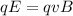
From which we get
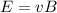
So the strength of the electric field must be
