PLEASE HELP ASAP are f(x)=4/x-2-1 and g(x)=3/x+2-2 inverses of each other?

Question

asked Apr 7, 2023 203k views

1 Answer

Bezzoon · Answer 1 · 2023-04-13T09:26:38+0000

Answer:

To find the inverse of:

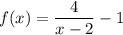
f (x)=(4)/(x-2)-1

Set the function to y:

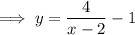
$\implies y=(4)/(x-2)-1$

Rearrange to make x the subject:

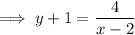
$\implies y+1=(4)/(x-2)$

$\implies (y+1)(x-2)=4$

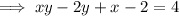
$\implies xy-2y+x-2=4$

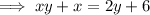
$\implies xy+x=2y+6$

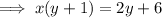
$\implies x(y+1)=2y+6$

$\implies x=(2y+6)/(y+1)$

Swap x and y:

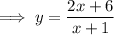
$\implies y=(2x+6)/(x+1)$

Change y to the inverse of the function sign:

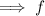
$\implies f$
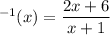
$\:^(-1)(x)=(2x+6)/(x+1)$

Rewrite g(x) as a fraction:

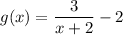
g(x)=(3)/(x+2)-2

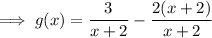
$\implies g(x)=(3)/(x+2)-(2(x+2))/(x+2)$

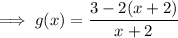
$\implies g(x)=(3-2(x+2))/(x+2)$

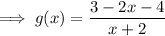
$\implies g(x)=(3-2x-4)/(x+2)$

$\implies g(x)=-(2x+1)/(x+2)$

Therefore, as the inverse of f(x) ≠ g(x), the functions are NOT inverses of each other