Question

If triangle ABC is similar to triangle DEC, find the values of x and y.

Answer 1

The values are x=8 and y=35, if the given ΔABC and ΔDEC are equal, it is obtained by Pythagoras theorem.

Explanation:

The given are,

From ΔABC,

AB= 6

BC= 10

AC = x

From ΔDEC,

CD= 28

DE= 21

CE = y

Step:1

Pythagoras theorem from ΔABC,

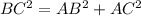`BC^(2)=AB^(2) + AC^(2)`...............(1)

Substitute the values,

`10^(2)` =
`6^(2)` +
`AC^(2)`

100 = 36 +
`AC^(2)`

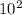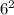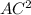
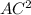
`AC^(2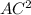)` = 100 - 36

= 64

AC =
`√(64)`

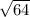
AC = 8

AC = x = 8

Step:2

Pythagoras theorem for ΔDEC,

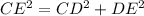`CE^(2) = CD^(2) + DE^(2)`................(2)

From the values,

`CE^(2)` =
`28^(2)` +
`21^(2)`

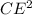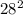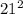
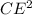`CE^(2)` = 784 + 441

= 1225

CE =
`√(1225)`

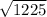
CE = 35

CE = y = 35

Result:

The values are x=8 and y=35, if the given ΔABC and ΔDEC are equal.