Question

According to the Mortgage Bankers Association, 8% of U.S. mortgages were delinquent in 2011. A delinquent mortgage is one that has missed at least one payment but has not yet gone to foreclosure. A random sample of eight mortgages was selected. What is the probability that exactly one of these mortgages is delinquent?

Answer 1

The probability that exactly one of these mortgages is delinquent is 0.357.

Explanation:

We are given that according to the Mortgage Bankers Association, 8% of U.S. mortgages were delinquent in 2011. A delinquent mortgage is one that has missed at least one payment but has not yet gone to foreclosure.

A random sample of eight mortgages was selected.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

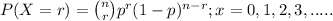
where, n = number of trials (samples) taken = 8 mortgages

r = number of success = exactly one

p = probability of success which in our question is % of U.S.

mortgages those were delinquent in 2011, i.e; 8%

LET X = Number of U.S. mortgages those were delinquent in 2011

So, it means X ~
`Binom(n=8, p=0.08)`

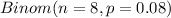
Now, Probability that exactly one of these mortgages is delinquent is given by = P(X = 1)

P(X = 1) =
`\binom{8}{1}* 0.08^(1) * (1-0.08)^(8-1)`

=
`8 * 0.08 * 0.92^(7)`

= 0.357

Hence, the probability that exactly one of these mortgages is delinquent is 0.357.