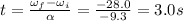Question

asked Oct 25, 2021 150k views

1 Answer

Lee Lowder · Answer 1 · 2021-10-28T13:55:47+0000

1)
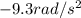
-9.3rad/s^2

2) 3.0 s

Step-by-step explanation:

1)

The angular acceleration of a rigid body in rotation can be found by using the equivalent of Newton's second law for rotational motions:

$\tau = I\alpha$ (1)

where

$\tau$ is the torque on the object

I is the moment of inertia of the object

$\alpha$ is the angular acceleration

Here we have:

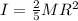I=(2)/(5)MR^2 is the moment of inertia of a solid sphere about its central axis, where

M = 240 g = 0.240 kg is the mass of the sphere

R = 4.50 cm /2= 2.25 cm = 0.0225 m is the radius of the sphere

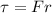$\tau = F r$ is the torque exerted by the frictional force, where

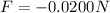F=-0.0200 N is the force of friction (negative because the direction is opposite to the motion)

r = R = 0.0225 m is the distance of the point of application of the force from the centre

Substituting into eq(1) we find

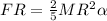
$FR=(2)/(5)MR^2 \alpha$

And solving for
$\alpha$ , we find the angular acceleration:

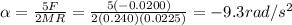
$\alpha = (5F)/(2MR)=(5(-0.0200))/(2(0.240)(0.0225))=-9.3rad/s^2$

2)

Here we know that the motion of the sphere is an angular accelerated motion.

Therefore, we can use the equivalent of suvat equations for rotational motion:

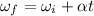
$\omega_f = \omega_i +\alpha t$

where

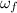$\omega_f$ is the final angular velocity

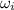$\omega_i$ is the initial angular velocity

$\alpha$ is the angular acceleration

t is the time

In this problem, we know that

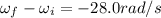$\omega_f-\omega_i = -28.0 rad/s$ , since we are told that the rotational speed decreases by 28.0 rad/s

$\alpha=-9.3 rad/s^2$ is the angular acceleration of the sphere

Solving for t, we find how long it takes for the sphere to decelerate by 28.0 rad/s:

$t=(\omega_f - \omega_i)/(\alpha)=(-28.0)/(-9.3)=3.0 s$

Please log in or register to add a comment.