Answer:
Distance to halfway point=45 km
Wilson's Time=5hrs
Joseph's time=6.26hrs
Explanation:
-Let x be the number of hours it takes for the two to meet halfway when Wilson starts his ride.
#The time already utilized prior to Wilson's start is:
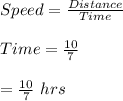
Joseph's remaining distance to the hallway point is less by 10km
Since, the distance to meet is equal, we equate their times as:

Hence, the distance ridden by each to the halfway point is 45 km
#We now use this distance to solve for individual times:
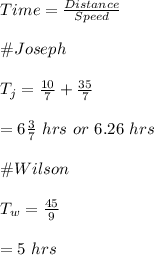
Hence, Joseph takes 6.26hrs while Wilson takes 5hrs to get to the halfway point.