Question

Which of the following are possible equations of a parabola that has no real solutions and opens downward?

y > = -(x + 4)^2- 2
y > = -(x + 4)^2 + 2
y > = -x^2 - 2
y > = (x - 4)^2 + 2
y > = -(x - 4)^2- 2

Answer 1

`y = - {(x - 4)}^(2) - 2`

`y = - {(x + 4)}^(2) - 2`

`y = - {x}^(2) - 2`

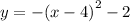
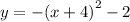
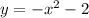
Explanation:

A vertex form equation of a parabola is of the form

`y = a(x - h)^(2) + k`

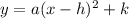
with vertex at (h,k).

If a parabola opens downwards, then a<0.

If the vertex of such parabola is below the x-axis, then it has no real solution, because it will not intersect the x-axis.

`y = - {(x + 4)}^(2) - 2`

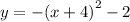
has vertex at (-4,-2), which is below x-axis.

`y = - {(x - 4)}^(2) + 2`

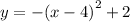
has vertex at (-4,2)--->above x-axis

`y = - {(x - 4)}^(2) - 2`

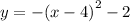
vertex at (4,-2) ---> below x-axis

`y = - {x }^(2) - 2`

(0,-2)----> below x-axis