Answer:
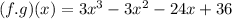
Domain of (f.g)(x) = All real numbers
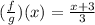
Domain of (f/g)(x) = All Real Numbers
Explanation:
Given functions are:
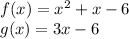
We have to calculate f.g and f/g
In order to find f.g we have to multiply both functions
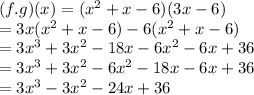
The domain of (f.g)(x) is all real numbers
Now
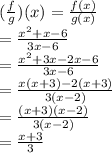
The domain of (f/g)(x) is all real numbers.
Hence,
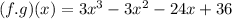
Domain of (f.g)(x) = All real numbers
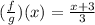
Domain of (f/g)(x) = All Real Numbers