Question

Let f(x) = x² + x - 6 and g(x) = 3x - 6, what are f ⋅ g and f/g. state the resulting function and it's domain.

Answer 1

`(f.g)(x) = 3x^3-3x^2-24x+36`

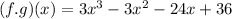
Domain of (f.g)(x) = All real numbers

`((f)/(g))(x) = (x+3)/(3)`

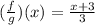
Domain of (f/g)(x) = All Real Numbers

Explanation:

Given functions are:

`f(x) = x^2+x-6\\g(x) = 3x-6`

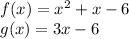
We have to calculate f.g and f/g

In order to find f.g we have to multiply both functions

`(f.g)(x) = (x^2+x-6)(3x-6)\\= 3x(x^2+x-6) - 6(x^2+x-6)\\= 3x^3+3x^2-18x-6x^2-6x+36\\= 3x^3+3x^2-6x^2-18x-6x+36\\=3x^3-3x^2-24x+36`

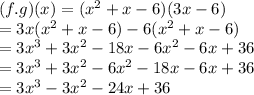
The domain of (f.g)(x) is all real numbers

Now

`((f)/(g))(x) = (f(x))/(g(x))\\= (x^2+x-6)/(3x-6)\\=(x^2+3x-2x-6)/(3x-6)\\=(x(x+3)-2(x+3))/(3(x-2))\\=((x+3)(x-2))/(3(x-2))\\=(x+3)/(3)`

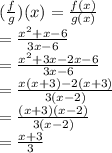
The domain of (f/g)(x) is all real numbers.

Hence,

`(f.g)(x) = 3x^3-3x^2-24x+36`

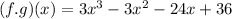
Domain of (f.g)(x) = All real numbers

`((f)/(g))(x) = (x+3)/(3)`

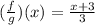
Domain of (f/g)(x) = All Real Numbers