Question

Principal value of Arccos(-1)

Answer 1

You may have wondered what Euler's Identity means

`e^(i \pi) = -1`

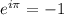
I hate to break it to you but it just means

`\cos \pi + i \sin \pi = -1 + 0i`

Equating respective real and imaginary parts,

`\cos \pi = -1, \qquad \sin \pi = 0`

which you probably already knew.

From the first part,

`\pi = \arccos(-1)`

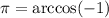
That's in the principal value range of cosine.

`\pi = \textrm{Arccos}(-1)`

Answer: π